Teurema da Menelao

Modell:O Modell:OCC Ul Teurema da Menelao l'è un teurema da Gieumetria elemantar ch'al trata di triangul.

Declarazziú

Dai un triangul ABC e tri pünt D, E e F chi stan in sö i rett BC, AC e AB rispetivament, D, E ed F a hin in fila se e domà se:

$\frac{AF}{FB}\cdot \frac{BD}{DC}\cdot \frac{CE}{EA}=-1.$

In questa equazziun, $AF$, $FB$, etc., i rapresentan i lünghez di segment cunt ul segn. Par esempi, la frazziun $AF/FB$ la g'haa segn pusitif domà quand che la reta par $D$, $E$ e $F$ la taja ul segment $AB$.

Sa tegn anca cuunt dul urientament di segment:

$AB=-BA$

Demustrazziú

Teurema du Menelao, cas 1: la reta DEF la taja no ul triangul ABC.

Teurema du Menelao, cas 2: la reta DEF la taja ul triangul ABC.

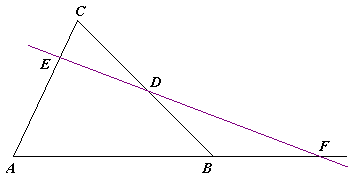
Sa veet che la aprt a sinistra du l'equazziun la g'haa segn negatif se tucc e tri i raport a hin negatif, cas in cui la reta $DEF$ la taja no ul triangul, o un raport l'è negatif e gli altar dü pusitif, cas in cui la reta $DEF$ la taja ul triangul in dü pünt (sa veda ul assioma da Pasch).

Sa disegnan i perpendicular da $A$, $B$ e $C$ in sö $DEF$, le ciami rispetivament $a$,$b$ e $c$. Mó par similitüdin da triangul, sa veet che:

$\left|\frac{AF}{FB}\right|=\left|\frac{a}{b}\right|,\left|\frac{BD}{DC}\right|=\left|\frac{b}{c}\right|,\left|\frac{CE}{EA}\right|=\left|\frac{c}{a}\right|$

Ciuè:

$\left|\frac{AF}{FB}\right|\cdot \left|\frac{BD}{DC}\right|\cdot \left|\frac{CE}{EA}\right|=|\frac{a}{b}\cdot \frac{b}{c}\cdot \frac{c}{a}|=1$

L'ültima uguaglianza la sa tröva semplificando i frazziuni dentar al modul.

Per l'oltar vers du l'implicazziun:

sian $D,E$ e $F$ in sö rispetivament i rett $BC,AC$ e $AB$, inscì che l'equazziun la vada ben. Sia $F^{\prime }$ ul pünt duè che i rett $DE$ e $AB$ sa tajan. Alura per quel ca sè demustrà in precedenza anca $D,E$ e $F^{\prime }$ i van ben in du l'equazziun. Sa cunfruntan:

$\frac{AF}{FB}=\frac{A{F}^{\prime }}{F^{\prime }B}$

Ma l'è mia pussibil che püssee d'un pünt al poo spezzà un segment in dü cunt un cert raport, sicchè sa cunclüd che:

$F=F^{\prime }.$